I've started playing a variant of chess called Atomic. The pieces move like traditional chess, and start in the same position. In this variant, however, when a piece takes another piece, both are removed from the board, as well as any non-pawn pieces on the (up to eight) adjacent squares. As a consequence of this one change, the game can end if your King is 'blown up' by your opponent's capture. As another consequence, Kings cannot capture, and may occupy adjacent squares.
For example, from the following position White's Knight can blow up the pawns at either d7 or f7, blowing up the Black King and ending the game.

I looked around for some resources on Atomic chess, but have never had luck with traditional chess studies. Instead I decided to learn about Atomic statistically.
As it happens, Lichess (which is truly a great site) publishes their game data which includes over 9 million Atomic games played. I wrote some code that will download and parse this data, turning it into a CSV file. You can download v1 of this file, but Lichess is the ultimate copyright holder.
First steps
The games in the dataset end in one of three conditions: Normal (checkmate or what passes for it in Atomic), Time forfeit, and Abandoned (game terminated before it began). The last category is very rare, and I omit these from my processing. The majority of games end in the Normal way, as tabulated here:
| termination | n |
|---|---|
| Normal | 8426052 |
| Time forfeit | 1257295 |
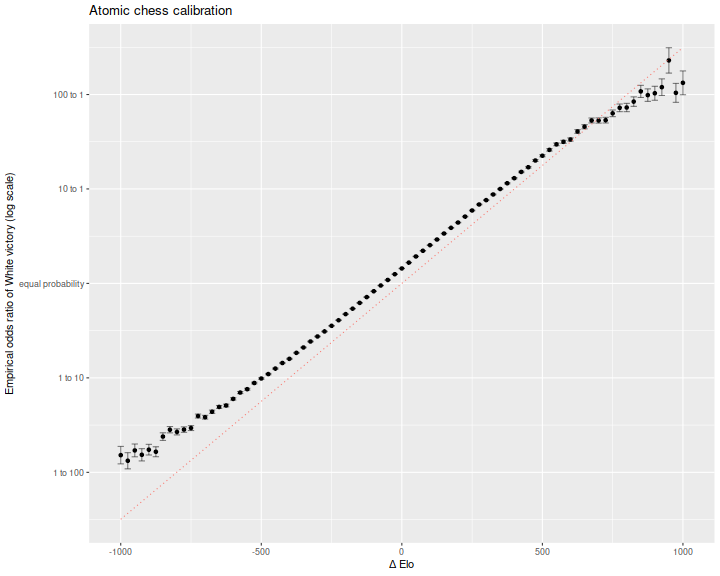
The game data includes Elo scores for players, as computed prior to the game. As a first check, I wanted to see if Elo is properly calibrated. To do this, I compute the empirical win rate of White over Black, grouped by bins of the difference in their Elo (again expressed from White's point of view). To avoid cases where the player is new to the system and their Elo has not yet converged to a good estimate, I select only matches where each player has already recorded at least 50 games in the database when the game is played. I also select for Normal terminations, since these are unambiguous victories. The remaining set contains 'only' 4692631 games.
Here is a plot of empirical log odds, versus Elo difference, in bins 25 points wide. This is in natural log odds space, so we expect the line to have slope of \(\operatorname{log}(10) / 400\) which is around 0.006. While the empirical data is nearly linear in Elo difference, it rides somewhat above the theoretical line. I believe this is due to a tempo advantage to White. If you want a boost, play White.
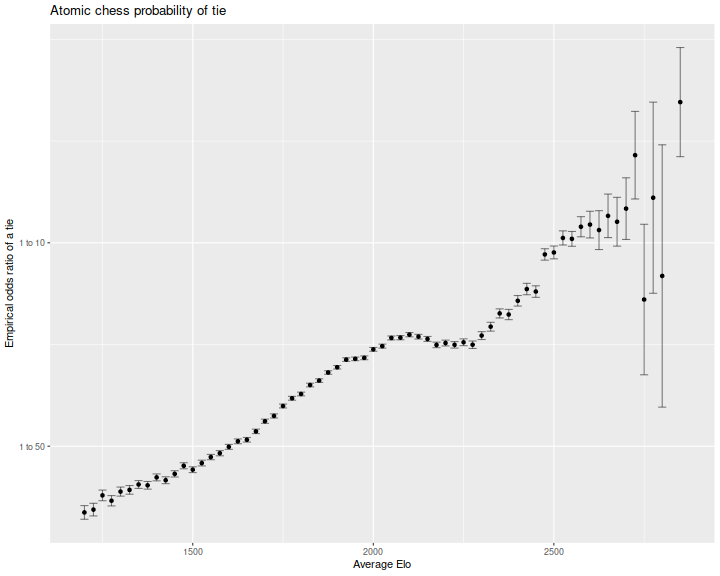
In competitive traditional chess, draws are quite common. In fact, the majority of championship games end in a draw. In a previous blog post I looked at calibrating the absolute Elo to the probability of a draw. This would prevent drift over time, meaning one could compare players from different generations. I was curious if a similar effect is seen in Atomic. Here is the ratio of odds of a tie, as a function of the average Elo of the two players. The log odds are mostly linear in average Elo, except for a curious dip around 2200. Perhaps many of these games end in a Time forfeit, which I exclude here.
Openings
My goal is to find good openings. However, there is a confounding variable of player ability. That is, a certain opening might look good only because good players tend to play it. (Perhaps the defining characteristic of good players is that they play good moves!) In traditional chess, a grand master could defeat me from any starting position, but in competition amongst themselves they most certainly avoid certain openings. So I wish to control for player ability, defined as the difference in Elo prior to the game.
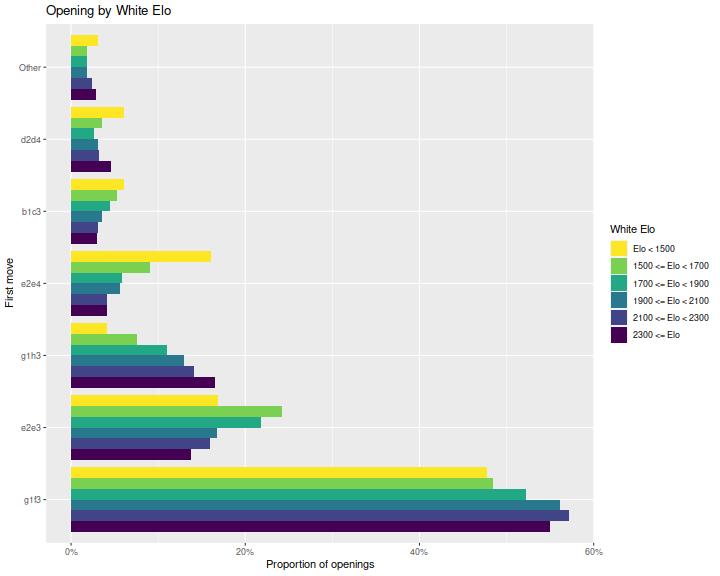
First let's look at the distribution of White's opening move.
Here are bar plots of the most frequent moves, grouped by
White's Elo.
Here I am only filtering on White's Elo and number of games in the database,
and consider all games, whether they terminate normally or by time forfeit.
We see that indeed, there are differences in choice of opening:
higher Elo players play g1f3 and g1h3 more often and e2e4 and e2e3 less
often than lower Elo players.
That said, these appear to be the four most common openings across
all players.
The Elo score is defined so that the log odds of victory from White's perspective is 10 to the Elo difference (White's minus Black's) divided by 400. The 400 is so that the units are palatable to humans. So if \(p\) is the probability that White will win a game, we should have
A statistician would view this as a logistic regression. Taking the natural log of both sides we have
To the right hand side we are going to add terms. First as a warm-up, we estimate White's tempo advantage by fitting to the specification
for some unknown \(b\). If instead we write this as
then the constant \(c\) is in 'units' of Elo.
I perform this regression on our data, removing Ties, players with few games and low Elo. Here is a table of the regression coefficients from the logistic regression, along with standard errors, the Wald statistics and p-values. I also convert the coefficient estimate into Elo equivalent units. White's advantage is equivalent to around 74 extra Elo points!
| term | estimate | std.error | statistic | p.value | Elo equivalent |
|---|---|---|---|---|---|
| (Intercept) | 0.425 | 0.002 | 270 | 0 | 74 |
| Elo | 0.006 | 0.000 | 675 | 0 | 1 |
Logistic analysis of opening moves
Of course, this is only if White does not squander their tempo. Some opening moves are likely to result in a higher boost to White than this average value, and some lower. I will now fit a model of the form
where \(1_{g1f3}\) is a 0/1 variable for whether White played g1f3 as their first move, and \(c_{g1f3}\) is the coefficient which we will fit by logistic regression. By rescaling by the magic number \(\operatorname{log}(10) / 400\), the coefficients \(c\) are denominated in 'Elo units'. Here is a table from that fit:
| term | estimate | std.error | statistic | p.value | Elo equivalent |
|---|---|---|---|---|---|
| Elo | 0.006 | 0.000 | 671.6 | 0 | 1 |
| g1h3 | 0.518 | 0.004 | 116.0 | 0 | 90 |
| g1f3 | 0.458 | 0.002 | 214.2 | 0 | 80 |
| e2e3 | 0.361 | 0.004 | 100.9 | 0 | 63 |
| e2e4 | 0.355 | 0.007 | 54.4 | 0 | 62 |
| d2d4 | 0.352 | 0.009 | 40.3 | 0 | 61 |
| b1c3 | 0.346 | 0.008 | 45.5 | 0 | 60 |
| Other | 0.092 | 0.010 | 8.8 | 0 | 16 |
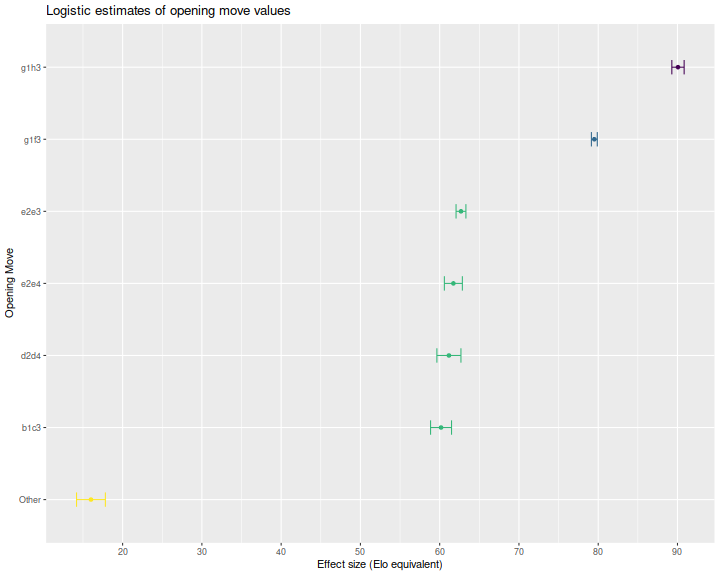
I also perform a multiple comparisons procedure on the opening move coefficients using Tukey's procedure to put them into equivalent groups. Here is a plot of the estimated coefficients, with error bars, colored by group. Again the coefficients are in Elo units. We see that g1h3 has a coefficient of around 90, while g1f3 is around 80. The four other openings considered are nearly equivalent, and all other moves are far inferior.
Second moves
This seems odd, however, because g1f3 is played much more often than g1h3, even by high Elo players. Moreover, just as White's apparent tempo advantage is the average value over a bunch of possible moves, some giving better results and some worse, so too is the boost from playing g1h3. Perhaps Black has a good refutation of this move, but it is not well known, and the effect we see here is an average over all of Black's replies.
So now I perform an analysis of Black's replies, conditional on White's opening. I filter for White's move, then perform a logistic regression, only considering the most frequent replies. Here is a table of the regression coefficients for the three best looking opening moves for White. Because the equations are still from White's point of view, Black would choose to play the move with the lowest Elo equivalent. Below we plot the coefficient estimates of Black's replies, again grouping statistically non-distinguishable coefficient estimates.
| move1 | move2 | estimate | std.error | statistic | p.value | Elo equivalent |
|---|---|---|---|---|---|---|
| e2e3 | Elo | 0.006 | 0.000 | 286.54 | 0 | 1.0 |
| e2e3 | d7d6 | 0.311 | 0.021 | 14.55 | 0 | 54.0 |
| e2e3 | e7e6 | 0.317 | 0.004 | 74.83 | 0 | 55.0 |
| e2e3 | d7d5 | 0.334 | 0.022 | 15.01 | 0 | 58.0 |
| e2e3 | g8f6 | 0.432 | 0.011 | 40.12 | 0 | 75.0 |
| e2e3 | e7e5 | 0.592 | 0.022 | 26.55 | 0 | 100.0 |
| e2e3 | Other | 0.763 | 0.016 | 48.37 | 0 | 130.0 |
| g1f3 | Elo | 0.006 | 0.000 | 490.63 | 0 | 1.0 |
| g1f3 | e7e5 | 0.135 | 0.007 | 19.25 | 0 | 24.0 |
| g1f3 | d7d6 | 0.145 | 0.017 | 8.46 | 0 | 25.0 |
| g1f3 | f7f6 | 0.483 | 0.002 | 211.38 | 0 | 84.0 |
| g1f3 | g8f6 | 0.834 | 0.048 | 17.50 | 0 | 140.0 |
| g1f3 | e7e6 | 1.458 | 0.047 | 30.81 | 0 | 250.0 |
| g1f3 | Other | 2.069 | 0.042 | 48.84 | 0 | 360.0 |
| g1h3 | Elo | 0.006 | 0.000 | 231.93 | 0 | 1.1 |
| g1h3 | e7e6 | 0.092 | 0.022 | 4.23 | 0 | 16.0 |
| g1h3 | e7e5 | 0.155 | 0.019 | 8.21 | 0 | 27.0 |
| g1h3 | f7f6 | 0.503 | 0.010 | 52.54 | 0 | 87.0 |
| g1h3 | h7h6 | 0.536 | 0.006 | 93.12 | 0 | 93.0 |
| g1h3 | Other | 0.554 | 0.024 | 22.75 | 0 | 96.0 |
| g1h3 | g7g5 | 1.837 | 0.037 | 49.63 | 0 | 320.0 |
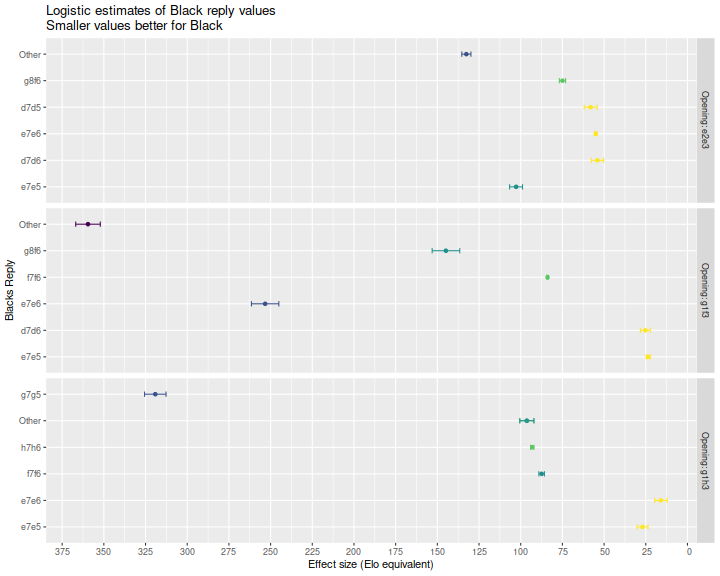
We note that the apparent best reply to g1f3 is e7e5, which yields an advantage to White of 24 Elo points; the best reply to e2e3 is d7d6, which is worth 54 Elo points to White; and the best reply to g1h3 is e7e6, which yields 16 Elo points. While our analysis of White's openings indicated that g1h3 is the best opening, this appears to be due to suboptimal replies from Black. To maximize the minimum reply from Black, White should apparently play e2e3.
I would take this analysis with a grain of salt. The response d7d6 to White's g1f3 looks very weak, with White taking Black's Queen and leaving Black's King very exposed. This suggests something very fishy with potential for big differences in optimal and average play in the responses.
Of course, there is also a horizon problem here. Just as the coefficient fits average over suboptimal play in Black's reply, our two level analysis ignores White's second move. In a future blog post I hope to perform a proper minimax analysis of openings, truncating the analysis when the data no longer supports different coefficient fits among the various possible moves, then minimaxing the values up. I also plan on performing a material value analysis, which is quite simple from the data available here. My early exploration suggests that the usual 1:3:3:5:9 point value system of Pawn, Knight, Bishop, Rook, Queen in traditional chess is not well calibrated to Atomic chess. Finally, I hope to catalog the many fool's mates and their frequency.