I recently saw a plot purporting to show the Rotten Tomatoes' 'freshness' rating of Robert De Niro movies over the years, with some chart fluff suggesting 'Bobby' has essentially been phoning it in since 2002, at age 59. Somehow I wrote and maintain a mirror of IMDb which would be well suited to explore questions of this kind. Since I am inherently a skeptical person, I decided to look for myself.
You talkin' to me?
First, we grab the 'acts in' table from the MariaDB via dplyr. I found
that working with dplyr allowed me to very quickly switch between in-database
processing and 'real' analysis in R, and I highly recommend it. Then we get
information about De Niro, and join with information about his movies,
and the votes for the same:
library(RMySQL)
library(dplyr)
library(knitr)
# get the connection and set to UTF-8 (probably not necessary here)
dbcon <- src_mysql(host='0.0.0.0',user='moe',password='movies4me',dbname='IMDB',port=23306)
capt <- dbGetQuery(dbcon$con,'SET NAMES utf8')
# acts in relation
acts_in <- tbl(dbcon,'cast_info') %>%
inner_join(tbl(dbcon,'role_type') %>%
filter(role %regexp% 'actor|actress'),
by='role_id')
# Robert De Niro, as a person:
bobby <- tbl(dbcon,'name') %>%
filter(name %regexp% 'De Niro, Robert$') %>%
select(name,gender,dob,person_id)
# all movies:
titles <- tbl(dbcon,'title')
# his movies:
all_bobby_movies <- acts_in %>%
inner_join(bobby,by='person_id') %>%
left_join(titles,by='movie_id')
# genre information
movie_genres <- tbl(dbcon,'movie_info') %>%
inner_join(tbl(dbcon,'info_type') %>%
filter(info %regexp% 'genres') %>%
select(info_type_id),
by='info_type_id')
# get rid of _documentaries_ :
bobby_movies <- all_bobby_movies %>%
anti_join(movie_genres %>%
filter(info %regexp% 'Documentary'),by='movie_id')
# get votes for all movies:
vote_info <- tbl(dbcon,'movie_votes') %>%
select(movie_id,votes,vote_mean,vote_sd,vote_se)
# votes for De Niro movies:
bobby_votes <- bobby_movies %>%
inner_join(vote_info,by='movie_id')
# now collect them:
bv <- bobby_votes %>% collect()
# sort it
bv <- bv %>%
distinct(movie_id,.keep_all=TRUE) %>%
arrange(production_year)
# save it for next time:
library(readr)
readr::write_csv(bv,'../data/bobby_deniro_data.csv')
Here, then is a plot of the average IMDb rating versus production year, with error bars at one standard error. To the naked eye there does appear to be a slight decline from a handful of great movies in the late 70s and 80s, but this is hardly a slam dunk. Note that user ratings of this form are known to be affected by selection biases: unless a movie is terrible, a viewer is less likely to write a review or rate a movie if they did not like it. Presumably the 'professional' critics whose views are aggregated by Rotten Tomatoes are not affected by this bias, since they are forced to review movies. It is also not clear how Rotten Tomatoes aggregated reviews from prior to, say, 1995, as this would involve combing through digitized archives of newspapers for reviews, hardly an error-free process, and subject to possible biases. Indeed, the IMDb ratings are also subject to a survivorship bias, as movies from before the internet age are not reviewed 'in real time', and only titles deemed worthy of DVD release or rebroadcast are seen and reviewed by a wide audience.
require(ggplot2)
library(ggrepel)
# select movies w/ > 500 votes
ph <- ggplot(bv %>% filter(votes > 500),aes(x=production_year,y=vote_mean,ymin=vote_mean-vote_se,ymax=vote_mean+vote_se,label=title)) +
geom_errorbar() +
stat_smooth() +
geom_text_repel(max.iter=500) +
geom_vline(xintercept=2002.5) +
labs(x='production year',y='average IMDb rating')
print(ph)
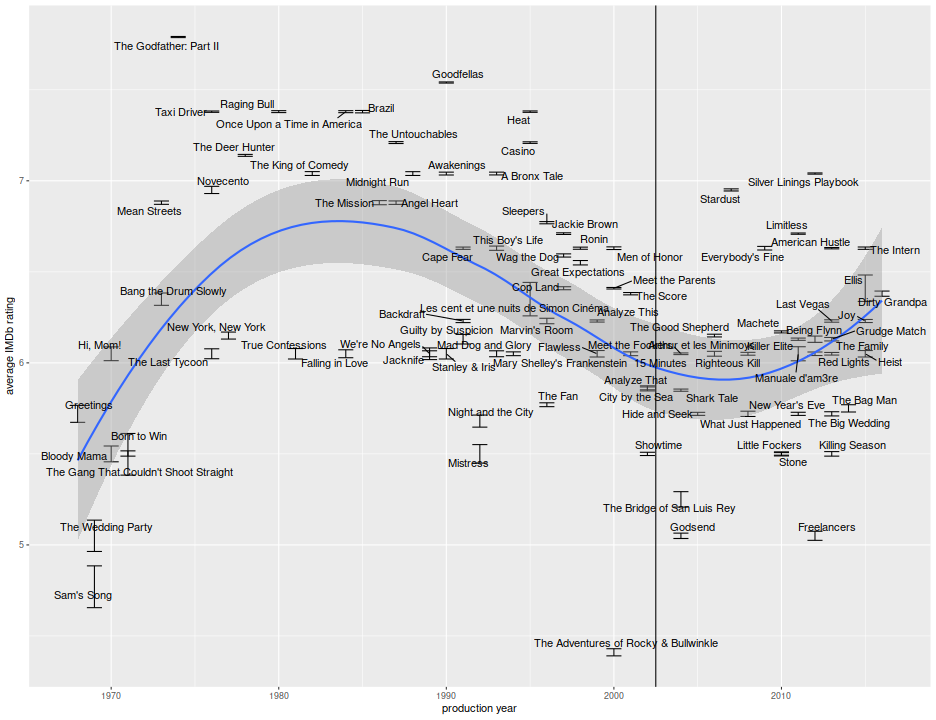
Ignoring the selection biases and disregarding the oddities of what an IMDb rating really means, I perform a regression test, basically an unpaired t-test with assumption of equal variance, for the presence of a 'structural break' (I always call this a Chow test, but maybe I should not) at the year 2002. I use both unweighted vanilla regression and a weighted least squares, with the latter taking into account the standard error of the mean vote. Both regressions find that the break is 'significant' at the 0.01 level, but the effect size is about half an IMDb star. That is, De Niro movies have an average rating of around 6.8, but more like 6.3 post 2002, according to the weighted regression. An unpaired t-test which does not assume equal variances also rejects the null with essentially the same conclusions.
bvdata <- bv %>%
filter(votes >= 1000) %>%
mutate(chowbreak = production_year > 2002)
mod0 <- lm(vote_mean ~ chowbreak,data=bvdata)
print(summary(mod0))
##
## Call:
## lm(formula = vote_mean ~ chowbreak, data = bvdata)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.0207 -0.3807 0.0252 0.4493 1.3593
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.431 0.080 80.43 <2e-16 ***
## chowbreakTRUE -0.406 0.132 -3.07 0.0028 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.604 on 88 degrees of freedom
## Multiple R-squared: 0.0969, Adjusted R-squared: 0.0867
## F-statistic: 9.45 on 1 and 88 DF, p-value: 0.00282
mod1 <- lm(vote_mean ~ chowbreak,data=bvdata,weights=1 / bvdata$vote_se)
print(summary(mod1))
##
## Call:
## lm(formula = vote_mean ~ chowbreak, data = bvdata, weights = 1/bvdata$vote_se)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -16.81 -5.15 -1.90 1.21 18.43
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.7637 0.0783 86.41 < 2e-16 ***
## chowbreakTRUE -0.5641 0.1256 -4.49 2.1e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.25 on 88 degrees of freedom
## Multiple R-squared: 0.187, Adjusted R-squared: 0.177
## F-statistic: 20.2 on 1 and 88 DF, p-value: 2.13e-05
mod2 <- t.test(x=bvdata[!bvdata$chowbreak,'vote_mean'][[1]],y=bvdata[bvdata$chowbreak,'vote_mean'][[1]])
print(mod2)
##
## Welch Two Sample t-test
##
## data: bvdata[!bvdata$chowbreak, "vote_mean"][[1]] and bvdata[bvdata$chowbreak, "vote_mean"][[1]]
## t = 3, df = 83, p-value = 0.001
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.164 0.648
## sample estimates:
## mean of x mean of y
## 6.43 6.02
In my experience, the IMDb rating scale is fairly non-uniform: a difference of half a star in rating is different at the high end than at the middle of the ratings, and so that half star difference might translate into a highly meaningful difference. I forget what the exact breaks were, but 6.8 might be the median rating, whereas 6.3 might be the first tertile. Again, those are not exact, but the range is somewhat compressed in the middle.
None of this is solid evidence to suggest that De Niro no longer cares, cannot remember his lines or whatever. There are numerous competing theories: movies are generally worse now, older actors cannot get good parts, the poor ratings were due to the directors or writers, and so on. I will consider some of these at a later date.