In a previous blog post I used logistic regression to estimate the values of pieces in Atomic chess. In that study I computed material differences between the two players using a snapshot 8 plies before the end of the match. (A "ply" is a move by a single player.) That choice of snapshot was arbitrary, but it is typically late enough in the match so there is some material difference to measure, and also near enough to the end to estimate the "power" of each piece to bring victory. However, this valuation is rather late in the game, and is probably not representative of the average value of the pieces. That is, a knight advantage early in the game could be parlayed into a queen advantage later, which could then prove decisive.
To fix that issue, I will re-perform that analysis on other snapshots. Recall that I am working from 9 million rated Atomic games that I downloaded from Lichess. For each match I selected a pseudo-random ply after the second and before the last ply of each game, uniformly. (There is no material difference before the third ply.) I also selected pseudo-random snapshots in the first third, the second third, and the last third of each match. I compute the difference in material as well as differences in passed pawn counts for each snapshot. You can download v2 of the data, and the code.
Recall that I am using logistic regression to estimate coefficients in the model
where \(\Delta e\) is the difference in Elo, and \(\Delta P, \Delta K, \Delta B, \Delta R, \Delta Q\) are the differences in pawn, knight, bishop, rook and queen counts. Here \(p\) is the probability that White wins the match. By putting the weird constant \(\operatorname{log}(10)/400\) in front of the expression, the constants \(c_P, c_K\) etc. are denominated in Elo equivalent units. Similarly, I fit a model with terms for passed pawn counts in various ranks.
As previously, I subselect to games where each player has already recorded at least 50 games in the database, where both players have pre-game Elo at least 1500, and games which are at least 10 ply in length.
Here is a table of the estimated coefficients for the four regressions, with coefficients and standard errors in Elo equivalents, as well as Wald statistics. The p-values all underflow to zero. The intercept term can be interpreted as White's tempo advantage.
| snapshot | term | Estimate | Std.Error | Statistic |
|---|---|---|---|---|
| random | Elo | 0.957 | 0.001 | 665.0 |
| random | White Tempo | 53.136 | 0.281 | 188.9 |
| random | Pawn | 31.301 | 0.329 | 95.0 |
| random | Knight | 47.058 | 0.471 | 99.9 |
| random | Bishop | 57.368 | 0.484 | 118.4 |
| random | Rook | 105.767 | 0.718 | 147.4 |
| random | Queen | 244.058 | 0.890 | 274.2 |
| first third | Elo | 1.006 | 0.001 | 710.2 |
| first third | White Tempo | 62.620 | 0.270 | 232.1 |
| first third | Pawn | 58.935 | 0.697 | 84.6 |
| first third | Knight | 83.380 | 0.878 | 95.0 |
| first third | Bishop | 76.827 | 0.986 | 77.9 |
| first third | Rook | 80.067 | 1.754 | 45.7 |
| first third | Queen | 148.910 | 1.768 | 84.2 |
| second third | Elo | 0.955 | 0.001 | 666.7 |
| second third | White Tempo | 50.868 | 0.283 | 179.5 |
| second third | Pawn | 38.063 | 0.322 | 118.3 |
| second third | Knight | 57.589 | 0.449 | 128.2 |
| second third | Bishop | 59.246 | 0.462 | 128.1 |
| second third | Rook | 107.305 | 0.742 | 144.7 |
| second third | Queen | 210.759 | 0.917 | 229.8 |
| last third | Elo | 0.915 | 0.001 | 619.6 |
| last third | White Tempo | 45.537 | 0.292 | 155.9 |
| last third | Pawn | 26.008 | 0.264 | 98.5 |
| last third | Knight | 32.499 | 0.397 | 81.8 |
| last third | Bishop | 55.957 | 0.396 | 141.2 |
| last third | Rook | 109.550 | 0.545 | 201.2 |
| last third | Queen | 283.669 | 0.716 | 396.1 |
The data are hard to digest in table form, so below I plot the coefficients for the four different snapshots, with standard error bars. We see that a queen is generally worth around 150-250 Elo points, a rook around 100 (though somewhat less early in the match), a bishop around 60 (more early in the match), a knight 30-80, and a pawn 15-60. As one progresses along the match (from first to second to last third), the queen and rook gain value, while the bishop, knight and pawn lose value.
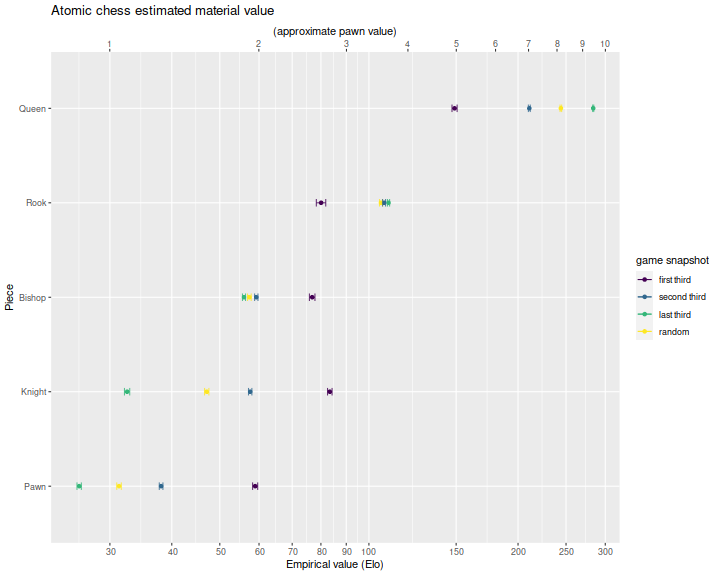
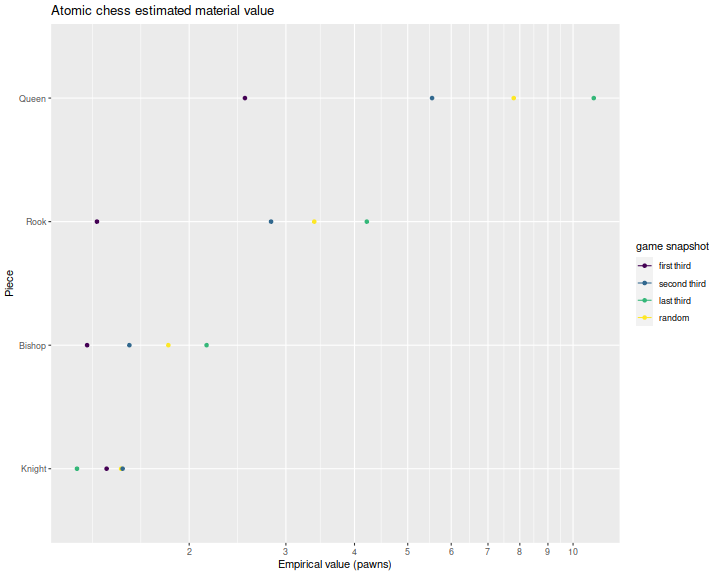
The top axis is denominated in 'pawn' units, where I eyeballed a pawn as worth around 30 Elo, but this is so variable over the different match snapshots it is hard to quote a consistent valuation scheme in pawn units. This is in contrast with the previous blog post where we suggested a 1:2.5:4:8:22 valuation for pawn, knight, bishop, rook, queen; that scheme is only appropriate for the very end of the match (and it can be hard to tell you are at the end of the match while playing). Below I denominate piece values relative to the estimated pawn values. (I drop the error bars because I am too lazy to code up the delta method.) For the random snapshot the pawn value estimates are as below
| Piece | Pawn value |
|---|---|
| Knight | 1.5 |
| Bishop | 1.8 |
| Rook | 3.4 |
| Queen | 7.8 |
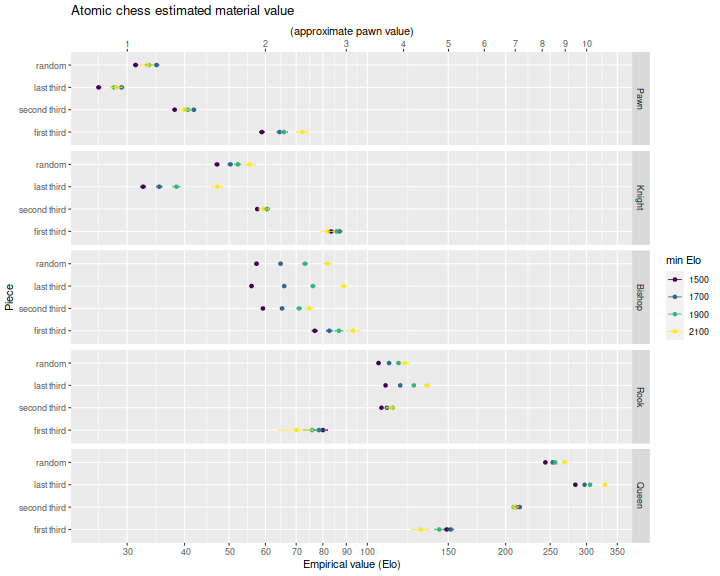
As in the previous blog post, I ran the regressions again with filters for minimum Elo. The reasoning is that better players will exhibit higher quality play, rather than average play. Here are plots by minimum Elo, snapshot and piece. We see that better players are better able to capitalize on bishops and perhaps knights, but otherwise the valuations are largely consistent across player ability.
Passed pawns
As in the previous blog post, I computed the difference in counts of passed pawns. I classified passed pawns as belonging to ranks 2, 3 or 4, to rank 5, to rank 6, or to rank 7; any pawn on rank 7 is automatically a passed pawn. When computing the material difference from White's point of view, the ranks are mirror image for Black in the obvious way. Again, I fit a model of the form
Here are the estimated regression coefficients and standard errors denominated in Elo,
along with the Wald statistics.
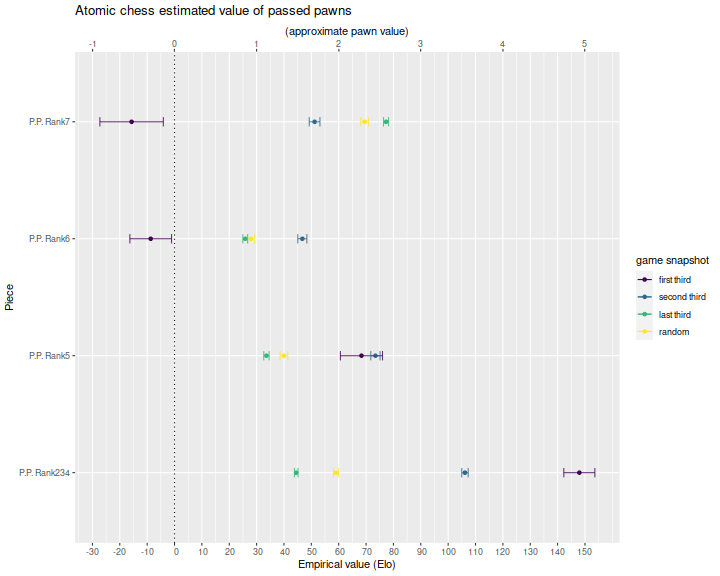
Below I plot the coefficients.
It should seem odd to you that high rank passed pawns can sometimes have negative value.
For example, a pawn on the seventh rank in the first third of a match appears to be
worth around -15 Elo.
The reason for this apparent contradiction is that this valuation is conditional on
taking a snapshot in the first third of a match, but in most situations if you have
a pawn on the 7th rank, it can often quickly lead to a victory. We are, however,
looking at those cases where it does not. For this analysis it probably
makes more sense to look at the random snapshot to get an "average" value.
| snapshot | term | Estimate | Std.Error | Statistic |
|---|---|---|---|---|
| random | Elo | 1.01 | 0.001 | 715.29 |
| random | White Tempo | 64.87 | 0.261 | 248.86 |
| random | P.P. Rank234 | 59.01 | 0.955 | 61.81 |
| random | P.P. Rank5 | 39.98 | 1.415 | 28.25 |
| random | P.P. Rank6 | 27.96 | 1.316 | 21.24 |
| random | P.P. Rank7 | 69.49 | 1.408 | 49.34 |
| first third | Elo | 1.02 | 0.001 | 719.17 |
| first third | White Tempo | 66.06 | 0.260 | 254.11 |
| first third | P.P. Rank234 | 147.94 | 5.674 | 26.07 |
| first third | P.P. Rank5 | 68.32 | 7.697 | 8.88 |
| first third | P.P. Rank6 | -8.71 | 7.618 | -1.14 |
| first third | P.P. Rank7 | -15.68 | 11.592 | -1.35 |
| second third | Elo | 1.01 | 0.001 | 715.28 |
| second third | White Tempo | 64.50 | 0.261 | 247.28 |
| second third | P.P. Rank234 | 106.15 | 1.174 | 90.42 |
| second third | P.P. Rank5 | 73.42 | 1.692 | 43.39 |
| second third | P.P. Rank6 | 46.71 | 1.655 | 28.22 |
| second third | P.P. Rank7 | 51.19 | 1.955 | 26.19 |
| last third | Elo | 1.01 | 0.001 | 711.41 |
| last third | White Tempo | 63.95 | 0.261 | 244.61 |
| last third | P.P. Rank234 | 44.47 | 0.651 | 68.36 |
| last third | P.P. Rank5 | 33.59 | 0.972 | 34.55 |
| last third | P.P. Rank6 | 25.85 | 0.888 | 29.10 |
| last third | P.P. Rank7 | 77.31 | 0.926 | 83.50 |
Spline Regressions
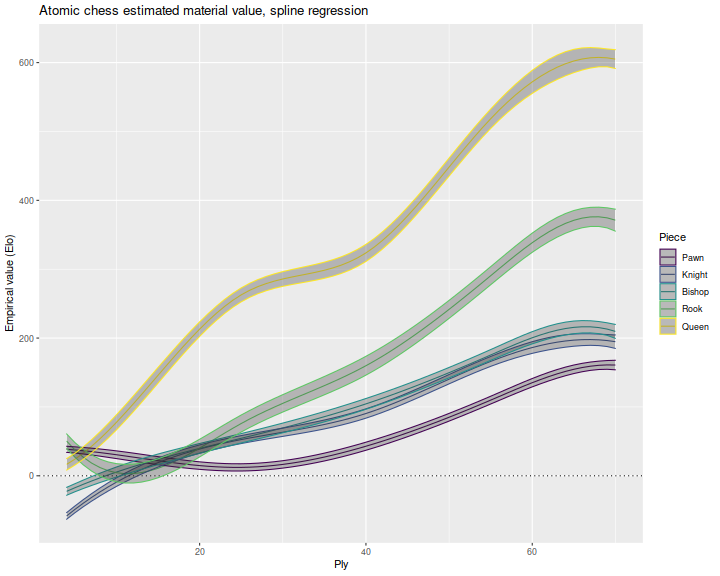
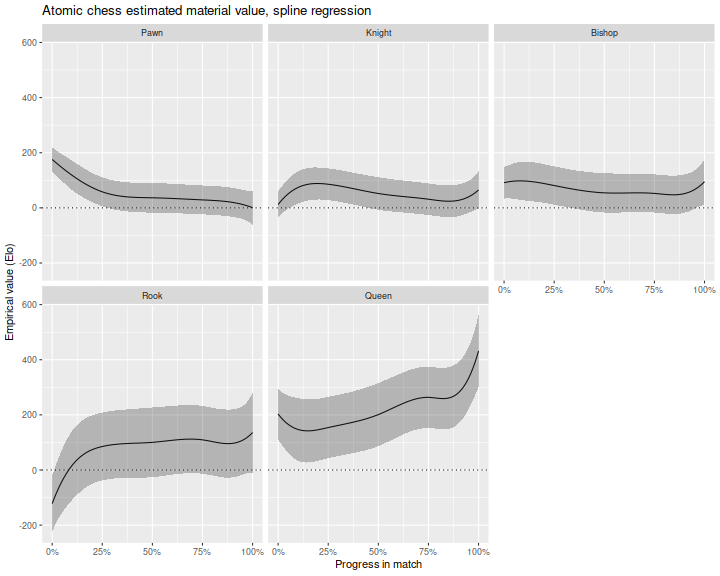
It is hard to interpret the coefficients because the value of pieces appears to depend on the phase of play. To remedy this, I interacted the material difference with some spline terms. That is, I compute some spline functions of the ply at which the snapshot is taken, the multiply those by the material differences. I then estimate the coefficients of the interaction terms, and combine them with the spline functions. This gives material value as a function of the ply, which I plot below. I did this two different ways: once computing splines over the raw ply, and then using the ply divided by the total ply. In the latter formulation you can view the valuation as percent progress in the match. The problem with this formulation is that you typically do not know how far along in the match you are. On the other hand, because matches progress at different speeds, basing value on the raw ply also seems flawed.
For the raw ply plot we plot in a single facet. For the percentage regression, this results in a visually unreadable plot, so we use separate facets for the different pieces. For the raw ply regression we see near equal values of the bishop and knight through most of the match; rooks increase in value after the 20th ply; queens are valuable from early in the match, and increase in value as the match progresses. This phenomenon is intuitive, as the queen is less likely to be captured later in the match when there are fewer pieces on the board.
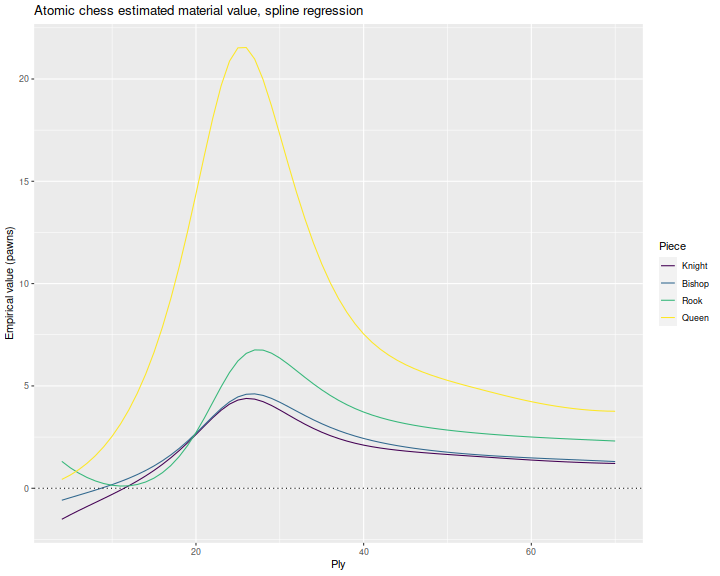
Below I express those estimates relative to the estimated value of a pawn. Again we lose the standard error bars. For the raw ply regression, we see a bulge at around 25 ply where pawns have very low value, and queens peak. A different pattern emerges in the percent ply regressions, where queens increase in value steadily over the course of the match.
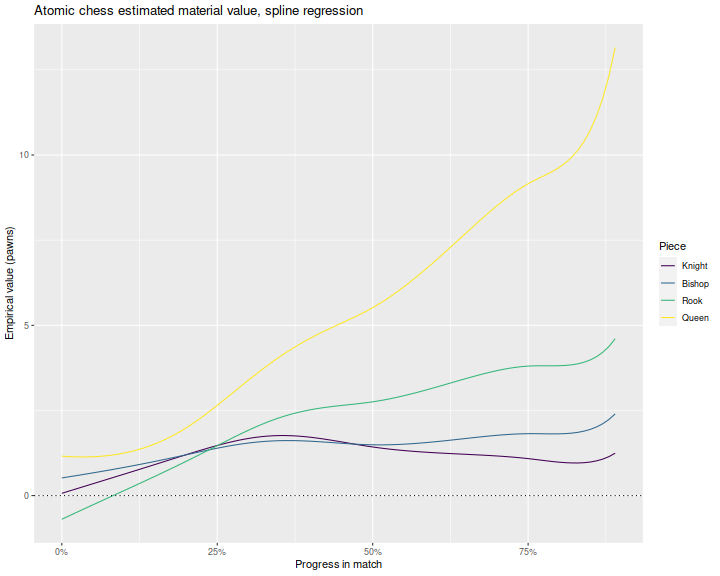
Future work
The analysis here indicates we need a better measure of match progress, one which can be computed in real time, but which matches the tempo of the particular match. It would seem that something like total material on the board would be a good measure. This is intuitive, as crowded positions are dangerous in Atomic and can quickly lead to large changes in the material difference. I also want to perform an analysis using survival analysis.