Most chess playing computer programs use forward search over the tree of possible moves.
Because such a search cannot examine every branch to termination of the game,
usually "static" evaluation of leaf nodes in the tree is via the combination of
a bunch of scoring rules.
These typically include a term for the material balance of the position.
In traditional chess the pieces are usually assigned scores of 1 point for pawns,
around 3 points for knights and bishops, 5 for rooks, and 9 for queens.
Human players often use this heuristic when considering exchanges.
I recently started playing a chess variant called Atomic chess. In Atomic, when a piece captures another, both are removed from the board, along with all non-pawn pieces in the up to eight adjacent squares. The idea is that a capture causes an 'explosion'. Lichess plays a delightful explosion noise when this happens.
The traditional scoring heuristic is apparently based on mobility of the pieces. While movement of pieces is the same in the Atomic variant, I suspect that traditional scoring is not well calibrated for Atomic: A piece can capture only once in Atomic; a piece can remove multiple pieces from the board in one capture; pieces have value as protective 'chaff'; Kings cannot capture pieces, so solo mates are possible; pawns on the seventh rank can trap high-value pieces by threatening promotion; there are numerous fools' mates involving knights, etc. Can we create a scoring heuristic calibrated for Atomic?
The problem would seem intractable from first principles, because piece value is so different from average piece mobility. Instead, perhaps we can infer a kind of average value for pieces. In a previous blog post I performed a quick analysis of Atomic openings on a database of around 9 million games played on Lichess. I used logistic regression to generalize Elo scores. Here I will pursue the same approach.
Suppose you took a snapshot of a game at some point, then computed the difference of White's pawn count minus Black's pawn count, White's knight count minus Black's, and so on. Let these be called \(\Delta P, \Delta K, \Delta B, \Delta R, \Delta Q.\) Let \(p\) be the probability that White wins the game. Let \(\Delta e\) be White's Elo minus Black's. I will estimate a model of the form
By putting the weird constant \(\operatorname{log}(10)/400\) in front of the expression, the constants \(c_P, c_K\) etc. are denominated in Elo equivalent units.
On reflection, I probably should have selected a random point uniformly over the lifetime of each match in my database to compute the material difference. Instead I selected four points to snapshot the material difference: just prior to the last move, two 'ply' prior to the match end, as well as four ply and eight ply. (In computer chess a 'ply' is a piece move by one player, while 'move' apparently refers to two ply.) This choice will have consequences, and I will have to consider the random snapshot approach if I ever write this up for real.
Regressions
I wrote some code that will download and parse Lichess' public data, turning it into a CSV file. You can download v1 of this file, but Lichess is the ultimate copyright holder. Here I will consider games which end by the 'Normal' condition (checkmate or what passes for it in Atomic). I subselect to games where each player has already recorded at least 50 games in the database. I also only take games where both players have pre-game Elo at least 1500. I also subselect to games which are at least 10 ply, which excludes many fool's mates.
Here is a table of the estimated coefficients, translated into Elo equivalents, as well as standard errors, Wald statistics and p-values (which all underflow to zero). The intercept term can be interpreted as White's tempo advantage, as outlined in the previous blog post.
| ply prior | term | Estimate | Elo equiv. | Std.Error | Statistic | P.value |
|---|---|---|---|---|---|---|
| 1 ply prior | Elo | 0.005 | 0.919 | 0.000 | 604.1 | 0 |
| 1 ply prior | White Tempo | 0.283 | 49.220 | 0.002 | 163.4 | 0 |
| 1 ply prior | Pawn | 0.054 | 9.447 | 0.002 | 36.1 | 0 |
| 1 ply prior | Knight | 0.161 | 27.889 | 0.002 | 69.0 | 0 |
| 1 ply prior | Bishop | 0.329 | 57.106 | 0.002 | 143.8 | 0 |
| 1 ply prior | Rook | 0.581 | 100.961 | 0.003 | 198.5 | 0 |
| 1 ply prior | Queen | 1.792 | 311.275 | 0.004 | 490.7 | 0 |
| 2 ply prior | Elo | 0.005 | 0.910 | 0.000 | 595.8 | 0 |
| 2 ply prior | White Tempo | 0.277 | 48.169 | 0.002 | 158.9 | 0 |
| 2 ply prior | Pawn | 0.074 | 12.882 | 0.002 | 48.2 | 0 |
| 2 ply prior | Knight | 0.191 | 33.185 | 0.002 | 80.9 | 0 |
| 2 ply prior | Bishop | 0.346 | 60.043 | 0.002 | 147.9 | 0 |
| 2 ply prior | Rook | 0.611 | 106.072 | 0.003 | 202.7 | 0 |
| 2 ply prior | Queen | 1.935 | 336.070 | 0.004 | 497.7 | 0 |
| 4 ply prior | Elo | 0.005 | 0.906 | 0.000 | 598.7 | 0 |
| 4 ply prior | White Tempo | 0.271 | 47.075 | 0.002 | 157.0 | 0 |
| 4 ply prior | Pawn | 0.095 | 16.581 | 0.002 | 61.2 | 0 |
| 4 ply prior | Knight | 0.196 | 34.109 | 0.002 | 82.3 | 0 |
| 4 ply prior | Bishop | 0.345 | 59.930 | 0.002 | 145.1 | 0 |
| 4 ply prior | Rook | 0.670 | 116.425 | 0.003 | 215.3 | 0 |
| 4 ply prior | Queen | 1.979 | 343.745 | 0.004 | 469.7 | 0 |
| 8 ply prior | Elo | 0.005 | 0.920 | 0.000 | 620.2 | 0 |
| 8 ply prior | White Tempo | 0.287 | 49.879 | 0.002 | 171.5 | 0 |
| 8 ply prior | Pawn | 0.109 | 18.981 | 0.002 | 67.4 | 0 |
| 8 ply prior | Knight | 0.318 | 55.225 | 0.003 | 126.3 | 0 |
| 8 ply prior | Bishop | 0.371 | 64.415 | 0.002 | 148.5 | 0 |
| 8 ply prior | Rook | 0.770 | 133.799 | 0.003 | 228.4 | 0 |
| 8 ply prior | Queen | 1.915 | 332.664 | 0.005 | 403.1 | 0 |
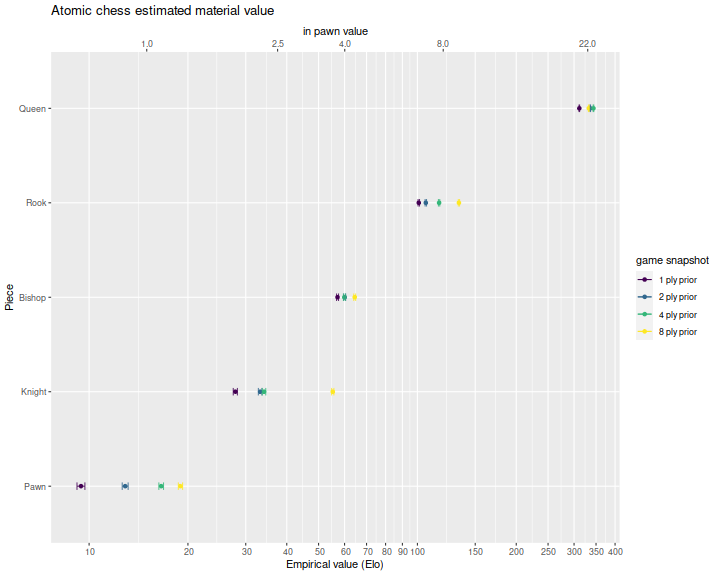
Below I plot these for the four different snapshots, with standard error bars. We see that a queen is generally worth around 300 Elo points (!), a rook around 100, a bishop around 60, a knight 30, and a pawn 15. As one gets closer to the end of the game (smaller ply prior), the pieces are generally worth less, which suggests there is typically some sacrifice of pieces for the winning side just prior to the last move.
The top axis is denominated in 'pawn' units, where I eyeballed a pawn as worth around 15 Elo. From this it seems that a knight is worth about 2.5 pawns, a bishop 4, a rook 8, and a queen 22. Note that knights appear to have higher value earlier in the game.
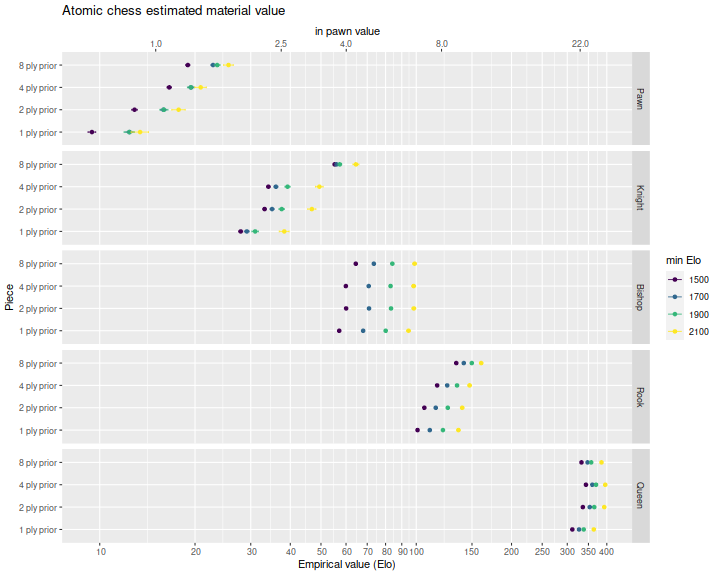
One problem I faced in the opening move analysis is that the regressions capture average play, not optimal play. That is, because of human error, tight time controls, and so on, there are many mistakes in the database. One way to try to control for that is to restrict to higher Elo players. This will add noise to the regressions because of the smaller sample size, but can perhaps give an indication of near-optimal value of pieces. So I re-ran the regressions, filtering on games where both players had greater than 1700 Elo, greater than 1900 and greater than 2100. I plot the regression coefficients below, with a different facet for each piece. We see that more skilled players are better able to take advantage of a material difference, and thus the pieces are worth more for the higher Elo matches. And perhaps bishops are more dangerous in the hands of a skilled player than an average player, worth perhaps 5 or 6 pawns. But otherwise the value of pieces under skilled play is close to that under average play, and certainly different from the piece values used in traditional chess.
Passed pawns
My data processing also computes the imbalance of passed pawns. A passed pawn is one which is not blocked by, or can be taken by an enemy pawn. In the figure below, the White pawn on d5 is a passed pawn. The Black pawn on b5 might be a passed pawn, depending on whether it can be taken en passant in the next move by White's pawn on a5.
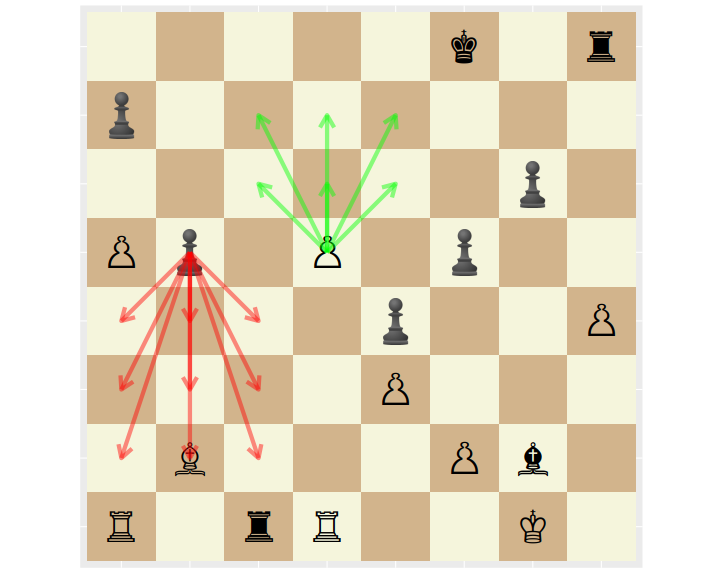
My processing does not take into account the en passant condition, as it was too tricky to implement, and unlikely to have much effect. I also group passed pawns as belonging to ranks 2, 3 or 4, to rank 5, to rank 6, or to rank 7. Any pawn on rank 7 is automatically a passed pawn. When computing the material difference from White's point of view, the ranks are mirror for Black in the obvious way. I fit a model of the form
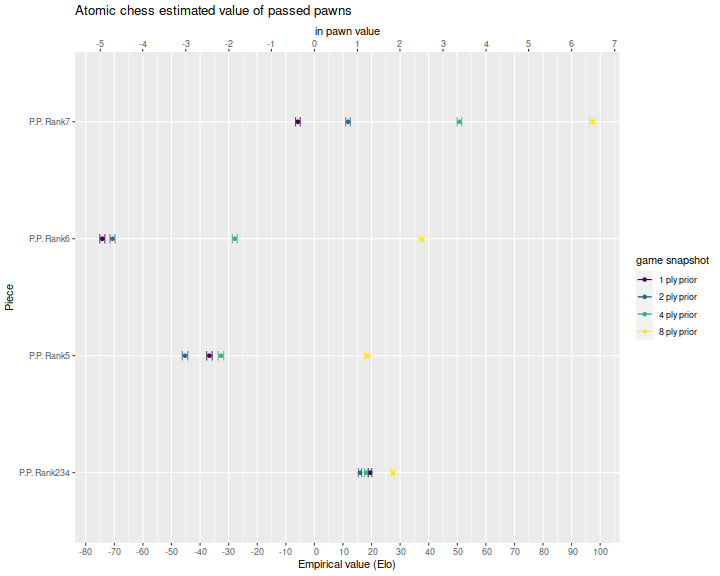
Here are the estimated regression coefficients, also denominated in Elo, along with the supporting statistics. Below I plot the coefficients. Not surprisingly, passed pawns are more valuable in the earlier snapshots, when there are more moves remaining until the end of game. This is because a passed pawn by itself is less of a threat to the king, than whatever major piece it might promote into. The negative values for snapshots close to the end of the game are a function of our selection mechanism. On average I expect passed pawns to have a net positive value.
| ply prior | term | Estimate | Elo equiv. | Std.Error | Statistic | P.value |
|---|---|---|---|---|---|---|
| 1 ply prior | Elo | 0.006 | 1.02 | 0.000 | 716.49 | 0 |
| 1 ply prior | White Tempo | 0.384 | 66.68 | 0.002 | 254.71 | 0 |
| 1 ply prior | P.P. Rank234 | 0.112 | 19.49 | 0.003 | 33.76 | 0 |
| 1 ply prior | P.P. Rank5 | -0.211 | -36.73 | 0.006 | -38.03 | 0 |
| 1 ply prior | P.P. Rank6 | -0.427 | -74.20 | 0.005 | -86.12 | 0 |
| 1 ply prior | P.P. Rank7 | -0.033 | -5.77 | 0.005 | -7.27 | 0 |
| 2 ply prior | Elo | 0.006 | 1.02 | 0.000 | 716.65 | 0 |
| 2 ply prior | White Tempo | 0.384 | 66.77 | 0.002 | 255.08 | 0 |
| 2 ply prior | P.P. Rank234 | 0.092 | 15.95 | 0.003 | 27.20 | 0 |
| 2 ply prior | P.P. Rank5 | -0.261 | -45.27 | 0.006 | -46.76 | 0 |
| 2 ply prior | P.P. Rank6 | -0.407 | -70.67 | 0.005 | -82.20 | 0 |
| 2 ply prior | P.P. Rank7 | 0.068 | 11.78 | 0.005 | 14.73 | 0 |
| 4 ply prior | Elo | 0.006 | 1.01 | 0.000 | 715.26 | 0 |
| 4 ply prior | White Tempo | 0.379 | 65.92 | 0.002 | 252.11 | 0 |
| 4 ply prior | P.P. Rank234 | 0.104 | 18.11 | 0.003 | 29.93 | 0 |
| 4 ply prior | P.P. Rank5 | -0.188 | -32.70 | 0.006 | -34.01 | 0 |
| 4 ply prior | P.P. Rank6 | -0.160 | -27.87 | 0.005 | -33.40 | 0 |
| 4 ply prior | P.P. Rank7 | 0.292 | 50.75 | 0.005 | 62.64 | 0 |
| 8 ply prior | Elo | 0.006 | 1.01 | 0.000 | 711.25 | 0 |
| 8 ply prior | White Tempo | 0.371 | 64.45 | 0.002 | 246.41 | 0 |
| 8 ply prior | P.P. Rank234 | 0.158 | 27.47 | 0.004 | 41.53 | 0 |
| 8 ply prior | P.P. Rank5 | 0.106 | 18.43 | 0.006 | 19.17 | 0 |
| 8 ply prior | P.P. Rank6 | 0.215 | 37.42 | 0.005 | 43.94 | 0 |
| 8 ply prior | P.P. Rank7 | 0.560 | 97.25 | 0.005 | 109.48 | 0 |
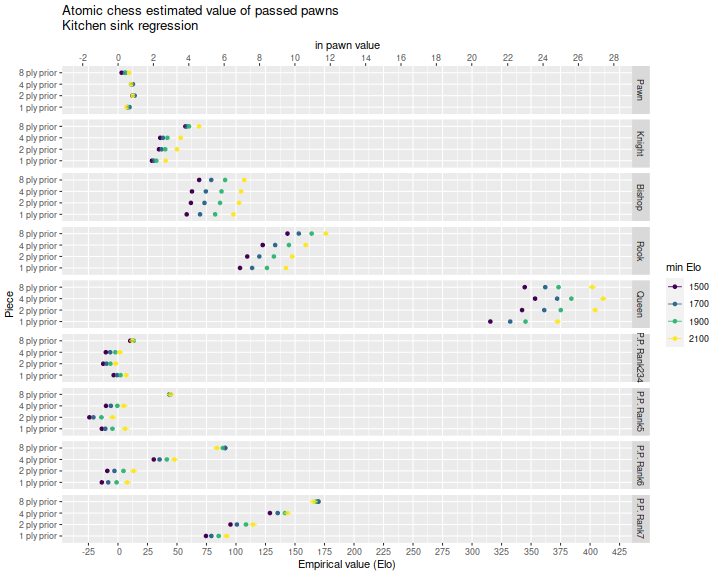
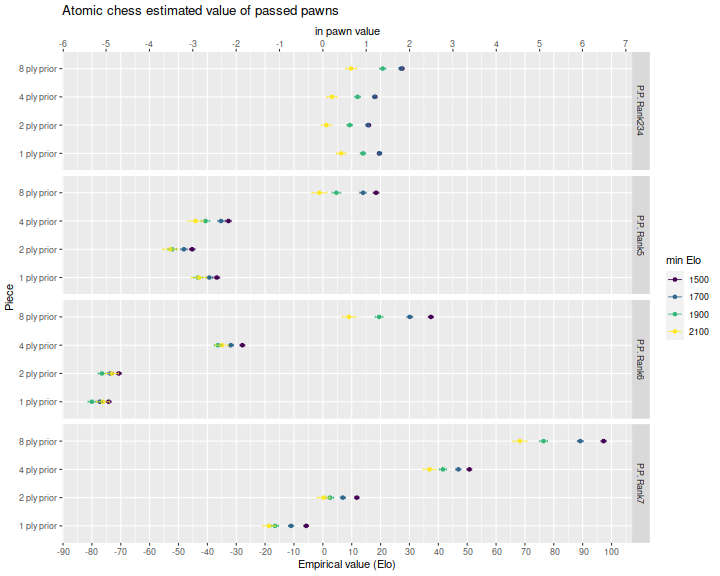
I perform the regressions on data filtered for minimum player Elo, as above. Below I plot the coefficients for a 1500, 1700, 1900 and 2100 minimum Elo limit. We see that passed pawns have somewhat lower value for games between skilled players, as presumably they can handle the threat better than average players.
I also performed 'kitchen sink' regressions with piece count differences and passed pawn count differences. Filtering by minimum Elo, the coefficients are plotted below. These do not change the regression results we see above by much, but one should recognize that pawn promotion means that passed pawn count and major piece count are not uncorrelated, and the regressions probably should be performed like this, with all terms included.