In a previous blog post I talked about two methods for dealing with conditioning information in portfolio construction. Here I apply them both to the problem of market timing with a discrete feature. Suppose that you have a single asset which you can trade long or short. You observe some 'feature', \(f_i\) prior to the time required to make an investment decision to capture the returns \(x_i\). In this blog post we consider the case where \(f_i\) takes one of \(J\) known discrete values. (note: this subsumes the case where one observes a finite number of different discrete features, since you can combine them into one discrete feature.)
The features are not something we can manipulate, and usually we consider them random (e.g. are we in a Bear or Bull market? are interest rates high or low? etc.), or if not quite random, at least uncontrollable (e.g. what month is it? did the FOMC just announce? etc.)
Denote the states by \(z_j\), and then assume that, conditional on \(f_i=z_j\) the expected value and variance of \(x_i\) are, respectively, \(m_j\) and \(s_j^2\). Let the probability that \(f_i=z_j\) be \(\pi_j\). Suppose that conditional on observing \(f_i=z_j\) you decide to hold \(w_j\) of the asset long or short, depending on the sign of \(w_j\). The (long term) expected return of your strategy is
and the (long term) variance of your returns are
Note that you can directly work with these equations. For example, it is relatively easy to show that you can maximize your signal-noise ratio, \(\mu/\sigma\) by taking
for some constant \(c\) chosen to achieve some long term volatility target. However, some of the analysis we might like to perform (are the weights different for different \(j\)? should we do this at all? etc.) is hard here because we have to start from scratch.
Flatten it!
This is a textbook case for "flattening", whereby we turn a conditional portfolio problem into an unconditional one. Let \(y_{i,j} = \chi_{f_i = z_j} x_i\) be the product of the indicator for being in the \(j\)th state, and the returns \(x_i\). Let \(w\) be the \(J\)-vector of your portfolio weights \(w_j\). The return of your strategy on the \(i\)th period is \(y_{i,\cdot} w\). Letting \(Y\) be the matrix whose \(i,j\)th element is \(y_{i,j}\), you can perform naive Markowitz on the sample \(Y\) to estimate \(w\).
But now you can easily perform inference: to see whether there is any "there there", you can compute the squared sample Sharpe ratio of the sample Markowitz portfolio, then essentially use Hotelling's \(T^2\) test. More interesting, however, is whether there is any additional gains to be had from market timing beyond the buy-and-hold strategy. This can be couched as the following portfolio optimization problem:
where \(g\) is some portfolio which we would like our portfolio to have no correlation to. Here the elements of the vector \(\mu\) are \(\pi_j m_j\), and the covariance \(\Sigma\) is \(\operatorname{diag}\left(d\right) - \mu\mu^{\top},\) where \(d_j = \pi_j \left(s_j^2 + m_j^2\right).\) To test whether market timing beats buy-and-hold, take \(g\) to be the vector of all ones, and then test the signal-noise ratio of the resultant portfolio. (n.b. This test is agnostic as to whether buy-and-hold long is better than buy-and-hold short!) That test is actually a "spanning test", and can be performed by using the delta method, as I outlined in section 4.2 of my paper on the distribution of the Markowitz portfolio.
Conditional Markowitz
In the conditional Markowitz procedure we force the \(s_j^2\) to be equal, while allowing the \(m_j\) to vary. To test this we construct a \(J\)-vector \(f_i\) of the indicator functions, then perform a linear regression of \(f_i\) against \(x_i\). Pooling the residuals of this in-sample fit, we then compute the estimate of \(s_{\cdot}^2\). Note that the conditional Markowitz portfolio now has \(w_j\) simply proportional to (our estimate of) \(m_j\), since the variance is fixed.
To test for presence of an effect one uses an MGLH test, like the Hotelling-Lawley trace. Now, however, the test for market timing ability beyond buy-and-hold is not via a spanning test. The spanning test outlined in section 4.5 of the asymptotic Markowitz paper only tests against other static portfolios on the assets, but in this case there is only a single asset, the market; To have zero correlation to the buy-and-hold portfolio one would have to hold zero dollars of the market. To test ability beyond buy-and-hold, one should use a regression test for equality of the regression betas, in this case equivalent to testing equality of all the \(m_j\). That is, an 'ANOVA'.
Lets try it
Here I demonstrate the idea with some toy data. The 'market' in this case are the monthly simple returns of the Market portfolio, taken from the Fama French data. I have added the risk-free rate back to the market returns as they were published by Ken French, since we may hold the Market long or short.
For features I compute the 6 month rolling mean return, and the 12 month volatility of Market returns. The mean computation is a bit odd, since these are simple returns, not geometric returns, and so they do not telescope. I lag both of these computations by two months, then align them with Market. The two month lag is equivalent to lagging the feature one month minus an epsilon, and is 'causal' in the sense that one could observe the features prior to making a trade decision.
I then binarize both these variables, comparing the mean to \(1\%\) per month to define the market as 'bear or 'bull', and comparing the volatility to \(4\%\) per square root month to define the environment as 'high vol' or 'low vol'. The product of these two give us a feature with four states. The odd cutoffs were chosen to give approximately equal \(\pi_j\). Here I load the data and compute the feature.
# devtools::install_github('shabbychef/aqfb_data')
library(aqfb.data)
data(mff4)
suppressMessages({
library(fromo)
library(dplyr)
library(tidyr)
library(magrittr)
})
df <- data.frame(mkt=mff4$Mkt) %>%
mutate(mean06=as.numeric(fromo::running_mean(Mkt,6,min_df=6L)),
vol12=as.numeric(fromo::running_sd(Mkt,12,min_df=12L))) %>%
mutate(vola=ifelse(dplyr::lag(vol12,2) >= 4,'hivol','lovol'),
bear=ifelse(dplyr::lag(mean06,2) >= 1,'bull','bear')) %>%
dplyr::filter(!is.na(vola),!is.na(bear)) %>%
tidyr::unite(feature,bear,vola,remove=FALSE)
Here are plots of the distribution of Market returns in each of the four states of the feature. On the top are the high volatility states; bear and bull are denoted by different colors. The violin plots show the distribution, while jittered points give some indication of the location of outliers.
library(ggplot2)
set.seed(1234)
ph <- df %>%
ggplot(aes(x=feature,y=Mkt,color=bear)) +
geom_violin() + geom_jitter(alpha=0.4,width=0.3,height=0) +
geom_hline(yintercept=0,linetype=2,alpha=0.5) +
coord_flip() +
facet_grid(vola~.,space='free',scales='free') +
labs(y='monthly market returns (pct)',
x='feature',
color='bear/bull market?',
title='market returns for different states')
print(ph)
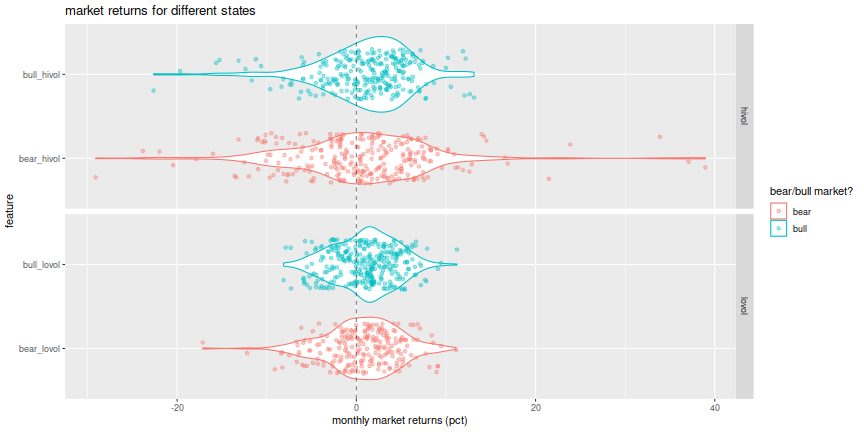
We clearly see higher volatility in the hivol case, but it is hard to
get a sense of how the mean differs in the four cases.
Here I tabulate the mean and standard deviation of returns
for each of the four states, and then compute the quasi Markowitz portfolio
defined as \(m_j/ \left(s_j^2 + m_j^2\right)\).
There is some momentum effect with higher Markowitz weights in bull
markets, and a low-vol effect due to autocorrelated heteroskedasticity.
library(knitr)
df %>%
group_by(feature) %>%
summarize(muv=mean(Mkt),sdv=sd(Mkt),count=n()) %>%
ungroup() %>%
mutate(`quasi markowitz`=muv / (sdv^2 + muv^2)) %>%
rename(`mean ret`=muv,`sd ret`=sdv) %>%
knitr::kable()
| feature | mean ret | sd ret | count | quasi markowitz |
|---|---|---|---|---|
| bear_hivol | 0.772418 | 7.90544 | 273 | 0.012243 |
| bear_lovol | 0.695631 | 4.09344 | 222 | 0.040350 |
| bull_hivol | 1.115115 | 5.03884 | 262 | 0.041869 |
| bull_lovol | 1.014484 | 3.41283 | 310 | 0.080028 |
Now let's perform inference.
Luckily I already coded all of the tests we will need here in SharpeR.
For flattening, take the product of the Market returns and the dummy
0/1 variables for the feature.
I then feed them to as.sropt, which computes and displays:
the Sharpe ratio of the Markowitz portfolio;
the "Sharpe Ratio Information Criterion" of
Paulsen and Sohl, which
is unbiased for the out-of-sample performance;
the 95 percent confidence bounds on the optimal Signal-Noise ratio;
the Hotelling \(T^2\) and associated \(p\)-value.
suppressMessages({
library(SharpeR)
library(fastDummies)
})
mktsr <- as.sr(df$Mkt,ope=12)
Y <- df %>%
dummy_columns(select_columns='feature') %>%
mutate(y_bull_hivol=Mkt * feature_bull_hivol,
y_bear_hivol=Mkt * feature_bear_hivol,
y_bull_lovol=Mkt * feature_bull_lovol,
y_bear_lovol=Mkt * feature_bear_lovol) %>%
select(matches('^y_(bull|bear)_(hi|lo)vol$'))
sstar <- as.sropt(Y,ope=12)
print(sstar)
SR/sqrt(yr) SRIC/sqrt(yr) 2.5 % 97.5 % T^2 value Pr(>T^2)
Sharpe 0.738 0.692 0.499 0.927 48.4 1.3e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
We compute the Sharpe ratio of the sample Markowitz
portfolio to be \(0.738022 \mbox{yr}^{-1/2}\).
Compare this to the Sharpe ratio of the long market
portfolio, which we compute to be around
\(0.585551 \mbox{yr}^{-1/2}\).
We now perform the spanning test.
This is via the as.del_sropt function,
where we feed in portfolios to hedge against.
We display the in-sample Sharpe statistic,
confidence intervals on the population quantity,
and the \(F\) statistic and \(p\) value.
spansr <- as.del_sropt(Y,G=matrix(rep(1,4),nrow=1),ope=12)
print(spansr)
SR/sqrt(yr) 2.5 % 97.5 % F value Pr(>F)
Sharpe 0.449 0.2 0.639 5.8 0.00062 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
We estimate the Sharpe of the hedged portfolio to be \(0.449229 \mbox{yr}^{-1/2}\). It is worth pointing out the subadditivity of SNR here. If you have two uncorrelated assets, the Signal-Noise ratio the optimal portfolio on the assets is the root square sum of the SNRs of the assets. Generalizing to \(k\) independent assets, the optimal SNR is the length of the vector whose elements are the SNRs of the assets. In this case we observe
which was the Sharpe of the unhedged timing portfolio. The gains beyond buy-and-hold seem modest indeed; one would require very patient investors to prove out this strategy in real trading.
SharpeR does not compute the portfolio weights.
So here I use MarkowitzR to compute and
display the weights of the unhedged Markowitz portfolio
and the Markowitz portfolio hedged against buy-and-hold.
The first should have weights proportional to the
quasi Markowitz weights shown above.
library(MarkowitzR)
bare <- mp_vcov(Y)
kable(bare$W,caption='unhedged portfolio')
Table: unhedged portfolio
| Intercept | |
|---|---|
| y_bull_hivol | 0.043931 |
| y_bear_hivol | 0.012845 |
| y_bull_lovol | 0.083913 |
| y_bear_lovol | 0.042368 |
vsbh <- mp_vcov(Y,Gmat=matrix(rep(1,4),nrow=1))
kable(vsbh$W,caption='hedged portfolio')
Table: hedged portfolio
| Intercept | |
|---|---|
| y_bull_hivol | 0.012535 |
| y_bear_hivol | -0.018551 |
| y_bull_lovol | 0.052517 |
| y_bear_lovol | 0.010972 |
The hedged portfolio has negative or near-zero weights in bear markets, and generally smaller holdings in high volatility environments, as expected. Note that we have achieved zero correlation to buy-and-hold without apparently having zero mean weights. In reality our portfolio weights have zero volatility-weighted mean.
All of this analysis was via the "flattening trick". I realize I do not have good tools in place to perform the spanning test in the conditional Markowitz formulation. Of course, R has tools for the ANOVA test, but they will not report the effect size in units like the Sharpe, so it is hard to interpret economic significance. However, I can easily compute the conditional Markowitz portfolio weights, which I tabulate below. Note that the assumption of equal volatility makes the portfolio weights proportional to the estimated mean returns
# conditional markowitz.
featfit <- mp_vcov(X=as.matrix(df$Mkt),
feat=df %>%
dummy_columns(select_columns='feature') %>%
select(matches('^feature_(bull|bear)_(hi|lo)vol$')) %>%
as.matrix(),
fit.intercept=FALSE)
kable(t(featfit$W),caption='conditional Markowitz unhedged portfolio')
Table: conditional Markowitz unhedged portfolio
| as.matrix(df$Mkt)1 | |
|---|---|
| feature_bear_hivol | 0.026648 |
| feature_bear_lovol | 0.023999 |
| feature_bull_hivol | 0.038471 |
| feature_bull_lovol | 0.034999 |
Caveats
I feel it is worthwhile to point out this is a toy analysis: the data go back to the late 1920's, which was a far different trading environment; we ignore any trading frictions and assume you can freely short or lever the Market; the feature is highly autocorrelated so investors are unlikely to see the long-term benefit of this timing portfolio, etc. In any case, don't take investing advice from a blogpost.
Further work
There is a non-parametric analogue of the flattening trick used here that applies to the case of market timing with a single continous feature, which I hope to present in a future blog post.