I cringe when I hear the term "Twelve Dimensional Chess" used as a metaphor. Certainly Twelve Dimensional Chess would be hard to visualize, and would present far more possible moves than regular two dimensional chess. However, high dimensional Chess suffers from a Curse of Dimensionality as the number of squares grows so quickly that play becomes uninteresting. In fact, I suspect that strategies exist which effectively guarantee a draw in sufficiently high dimensions.
Consider a Queen attacking a King in our stupid old Two Dimensional Chess. The Queen can cover or attack seven of the nine squares available to the King, as shown below:
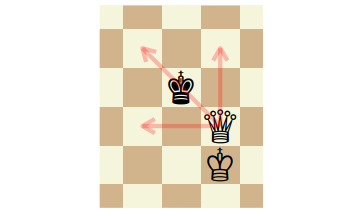
If the two remaining squares are occupied, or do not exist because the King is against the boundary, the Queen can give checkmate.
However, in higher dimensional Chess, the Queen attacks a far smaller proportion of the squares adjacent to a King. In dimension \(d\) the number attacked or covered is \(2^{d+1} - 1\). For \(d=12\), the number of squares attacked is \(8191\). However, the King has \(3^{12}=531441\) squares in his neighborhood when not against the boundary. The queen covers only about \(1.54\%\) of these squares, so you would need \(65\) Queens to give checkmate. A non-losing strategy seems to be:
Move your King away from the boundary on your first move, and keep away from the boundary. Your opponent cannot promote enough pawns to give checkmate.
Actually, I do not know the rules of high dimensional Chess, and I have assumed the players start with eight pieces and eight pawns. Maybe the number of pawns is linear, or even exponential in the dimension. Even so, it will take over \(300\) moves to promote the \(64\) pawns to Queens. Moreover, assuming one's opponent could muster such an army without any losses, assembling such a large number of Queens in place to achieve checkmate might be tricky. Each Queen attacks at most \(1.86\) million squares. Again, this would be hard to visualize during play, but there are \(2.2\) billion internal squares (i.e. those not touching a boundary), and some \(68.7\) billion in total. Which means that even if your opponent has dozens of Queens on the board, each Queen can attack only a small fraction of the available squares. You could move your King largely at random without coming under attack.
So "Twelve Dimensional Chess" as a metaphor for a situation requiring great foresight or strategy in the face of many possible decision is flawed. Instead, it is a more apt metaphor for a very lonely random walk punctuated by infrequent interactions with others you can easily dodge.
See also John D. Cook on 3D Knight Moves.