I received some taster ratings from the champagne party we attended last week. I joined the raw ratings with the bottle information to create a single aggregated dataset. This is a 'non-normal' form, but simplest to distribute. Here is a taste:
library(dplyr)
library(readr)
library(knitr)
champ <- read_csv('../data/champagne_ratings.csv')
champ %>% select(winery,purchase_price_per_liter,raternum,rating) %>%
head(8) %>% kable(format='markdown')
| winery | purchase_price_per_liter | raternum | rating |
|---|---|---|---|
| Barons de Rothschild | 80.00000 | 1 | 10 |
| Onward Petillant Naturel 2014 Malavasia Bianca | 33.33333 | 1 | 4 |
| Chandon Rose Method Traditionnelle | 18.66667 | 1 | 8 |
| Martini Prosecco from Italy | 21.32000 | 1 | 8 |
| Roederer Estate Brut | 33.33333 | 1 | 8 |
| Kirkland Asolo Prosecco Superiore | 9.32000 | 1 | 7 |
| Champagne Tattinger Brute La Francaise | 46.66667 | 1 | 6 |
| Schramsberg Reserver 2001 | 132.00000 | 1 | 6 |
Recall that the rules of the contest dictate that the average rating of each
bottle was computed, then divided by 25 dollars more than the
price (presumably for a 750ml bottle). Depending on whether the average
ratings were compressed around the high end of the zero to ten scale,
or around the low end, one would wager on either the cheapest bottles, or more
moderately priced offerings. (Based on my
previous analysis, I brought the
Menage a Trois Prosecco, rated at 91 points, but available at Safeway for
10 dollars.) It is easy to compute the raw averages using dplyr:
avrat <- champ %>%
group_by(winery,bottle_num,purchase_price_per_liter) %>%
summarize(avg_rating=mean(rating)) %>%
ungroup() %>%
arrange(desc(avg_rating))
avrat %>% head(8) %>% kable(format='markdown')
| winery | bottle_num | purchase_price_per_liter | avg_rating |
|---|---|---|---|
| Desuderi Jeio | 4 | 22.66667 | 6.750000 |
| Gloria Ferrer Sonoma Brut | 19 | 20.00000 | 6.750000 |
| Roederer Estate Brut | 12 | 34.66667 | 6.642857 |
| Charles Collin Rose | 34 | 33.33333 | 6.636364 |
| Roederer Estate Brut | 13 | 33.33333 | 6.500000 |
| Gloria Ferrer Sonoma Brut | 11 | 21.33333 | 6.400000 |
| Kirkland Asolo Prosecco Superiore | 16 | 9.32000 | 6.375000 |
| Mumm Napa Brut Rose | 24 | 26.66667 | 6.285714 |
The average ratings range between 3.6666667 and 6.75, so based on my previous analysis, one expects that the winner will be moderately priced, around 7 to 12 dollars in price. But something funny happened: the average ratings do not appear to be positively correlated with cost. Consider the Kendall \(\tau\) measure of correlation, which tests for the presence of a monotonic relationship between paired observations:
cor(avrat$avg_rating,avrat$purchase_price_per_liter,method='kendall')
## [1] -0.06176777
You can check for significance (only if you're a Frequentist) using the
cor.test function. There are a number of issues around this, however:
- Because of the design of this 'experiment', the errors in the taster ratings are not independent. This occurs because idiosyncratic rater preferences affect some champagnes more than others.
- Similarly, the errors in ratings are heteroskedastic, since some champagnes were rated by more raters than others.
- As a practical matter, there are ties in the average ratings, so
cor.testwill complain unless you read the man page and tweak the default settings at your own peril.
Modulo these warnings, it is hard to see the negative \(\tau\) as evidence in favor of a positive relationship between perceived tastiness and price.
Give me a Z?
Since inter-rater reliability is likely to be a problem (I intentionally shifted my average rating downward to increase my own chances of winning, an attack possible in this experiment even under taster blinding), I also tried to normalize ratings for the rater's bias. So I subtract each rater's mean rating, then compute bottle averages. I would have computed a Z-score, but many of the raters tasted fewer than 10 champagnes, making the standard deviations unreliable. Under this adjusted average, the top bottles do not change much, but notice that the duplicated Gloria Ferrer Sonoma Brut bottles have closer adjusted ratings.
avrat <- champ %>%
group_by(raternum) %>%
mutate(rating=rating-mean(rating)) %>%
ungroup() %>%
group_by(winery,common_name,bottle_num,purchase_price_per_liter) %>%
summarize(adj_rating=mean(rating)) %>%
ungroup() %>%
left_join(avrat %>% select(bottle_num,avg_rating),by='bottle_num') %>%
arrange(desc(adj_rating))
avrat %>% select(winery,bottle_num,purchase_price_per_liter,adj_rating) %>%
arrange(desc(adj_rating)) %>%
head(8) %>% kable(format='markdown')
| winery | bottle_num | purchase_price_per_liter | adj_rating |
|---|---|---|---|
| Desuderi Jeio | 4 | 22.66667 | 1.5516168 |
| Gloria Ferrer Sonoma Brut | 11 | 21.33333 | 0.9608738 |
| Gloria Ferrer Sonoma Brut | 19 | 20.00000 | 0.9151328 |
| Roederer Estate Brut | 13 | 33.33333 | 0.9002145 |
| Gloria Ferrer Blanc De Blancs | 20 | 26.65333 | 0.8590897 |
| Mumm Napa Brut Rose | 24 | 26.66667 | 0.8302900 |
| Kirkland Asolo Prosecco Superiore | 16 | 9.32000 | 0.8048640 |
| Piper Sonoma Blanc de Blancs | 26 | 15.98667 | 0.7445296 |
Kendall's \(\tau\) is now even more damning of a positive relationship between
price and 'tastiness'. I will not show the results of cor.test, since the
assumptions of that test are even more questionable.
cor(avrat$adj_rating,avrat$purchase_price_per_liter,method='kendall')
## [1] -0.1503823
Get Me an Expert!
Remember that my entire strategy for winning this contest was predicated on using the 'expert' ratings, publicly available, to predict ratings. Could I have missed this antipathy towards price? Let's check the Kendall \(\tau\) for the 'pro' ratings:
pros <- read_csv('../data/champagne.csv')
pros$pro_rating <- rowMeans(pros[,c('WS','WE','WandS','WW','TP','JS','ST')],na.rm=TRUE)
cor(pros$pro_rating,pros$price_per_liter,use='complete.obs',method='kendall')
## [1] 0.5944033
Let us stipulate that this value is significantly positive. There are two possible interpretations for this outcome, one of which seems like a total conspiracy theory:
- Expert tasters are better able to taste true quality in Champagne.
- Experts are not blind to the price of what they taste, and the entire purpose of ratings is to justify spending more on a bottle of Champagne than you might otherwise.
I won't say which is the conspiracy theory. Let us, however, look at the pro ratings versus our taster ratings (the 'hoi polloi'), Z-scoring the ratings for both groups. There does seem to be a serious mismatch between these two functions of price:
group_ratings <- avrat %>%
select(purchase_price_per_liter,adj_rating) %>%
rename(price=purchase_price_per_liter) %>%
mutate(rater='hoi polloi') %>%
rbind(pros %>% select(price_per_liter,pro_rating) %>%
rename(price=price_per_liter,adj_rating=pro_rating) %>%
mutate(rater='expert')) %>%
group_by(rater) %>%
mutate(adj_rating=(adj_rating - mean(adj_rating,na.rm=TRUE))/sd(adj_rating,na.rm=TRUE))
library(ggplot2)
ph <- ggplot(group_ratings,aes(x=price,y=adj_rating,group=rater,colour=rater)) +
geom_point() +
stat_smooth() +
scale_x_log10() +
labs(x='price per liter',y='rating (Z)')
print(ph)
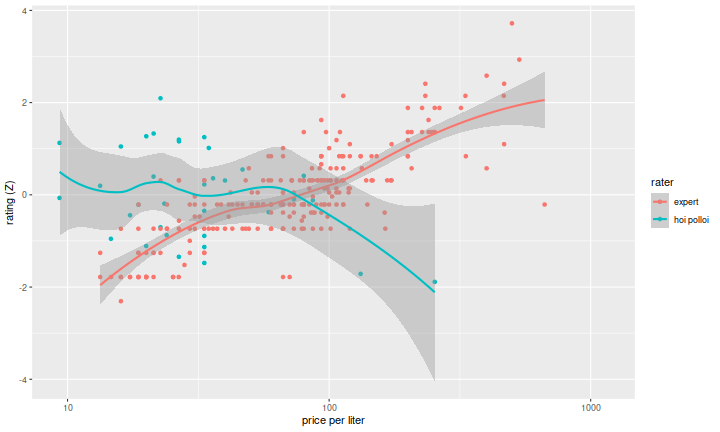
Computing the Kendall \(\tau\) on bottles which appear in both experiments would be enlightening, but there are actually very few in the intersection, due to mismatches in vintage and style, and also the mismatch in price points of the two groups. I think it should not be surprising that the cheapest sparkling wines scored relatively well among real tasters--a cheaper product should have broad appeal in order to make up for the presumably smaller margins.
Conclusions
If you are on the market for a bottle of Champagne, say to bring to a New Year's party, here are my suggestions based on the limited data available:
- Spend around 13 dollars for a 750ml bottle.
- If I had to guess, among the cheapest sparkling wines, the drier style is likely to be more palatable than the sweeter styles.
- If you feel embarrassed bringing a cheap bottle to someone's party, buy two bottles. Or, better, bring flowers too.